In 1959, Donald T. Campbell and Donald W. Fiske published an article in the Psychological Bulletin that, approximately 30 years later, would become the most cited article in the history of the social sciences. By 1992, it had been cited more than 2,000 times by other authors, and a 2005 search of the Social Sciences Citation Index showed more than 4,000 citations. The subject of this article was a statistical tool known as the multitrait-multimethod (MTMM) matrix. An MTMM matrix is a matrix of correlation coefficients computed between each pair of a set of measures (the correlation coefficients indicate how strongly each pair of measures is related).
The correlation matrix is intended to evaluate psychological measures—it is used to help determine how well scores on the measures actually reflect the intended traits. For example, personality traits such as extroversion and conscientiousness are often measured by self-reports, but they could also be measured by reports from others (e.g., friends or coworkers). If all psychological measurements were perfectly accurate, we would not need to consider different methods because all would be identical. But measurements are never perfect; they can be influenced by a variety of factors in addition to the intended traits (e.g., a person’s self-assessments of personality might partially reflect that person’s idealized view of him- or herself instead of his or her actual personality). The MTMM matrix is designed to evaluate the extent to which measures are influenced by the intended traits versus other systematic factors, commonly referred to as method effects.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
Industrial and organizational psychologists have made extensive use of the MTMM matrix. They have conducted large-scale reviews of MTMM studies of job affect and perceptions (using different standard surveys as methods), job performance ratings (using performance dimensions as traits and rating sources such as supervisors and peers as methods), and assessment centers (a set of exercises used to assess potential or current workers; the assessment dimensions serve as traits and the exercises serve as methods). Individual studies have focused on other topics, such as measuring personality. In many cases, the studies indicate substantial method variance—for example, job performance ratings are fairly heavily influenced by the perspective of the particular individual providing the ratings.
Computing the MTMM matrix begins with a study in which multiple traits are measured by multiple methods. This might mean that a sample of people are asked to complete a survey rating their own personality traits, and their personalities are also rated on the same survey by close friends and then again by coworkers. If, for example, five personality traits are measured by these three methods, there would be a total of 15 measures (five traits x three methods). The MTMM matrix can then be computed.
In their original paper, Campbell and Fiske described two main components of validity that, when taken together, provide information on the overall validity of the measures. One component is convergent validity. This means that two measures of the same trait, provided by different methods, should converge on the same conclusion. If ratings of personality are valid, then reports of extroversion by friends and coworkers should tend to agree about how extroverted the person is. A second criterion is discriminant validity.
This means that measures of different traits should be distinct. When rating someone’s personality, a friend or coworker should distinguish between that person’s extroversion and his or her conscientiousness.
Statistical evaluation of the MTMM matrix is fairly complex, and there is no consensus that there is any single best way to do it. Table 1 shows a sample matrix from Campbell and Fiske’s 1959 article in which five personality traits are rated for clinical psychology students living together in teams and participating in assessment exercises. Ratings of personality were provided by staff members, teammates, and the students themselves.
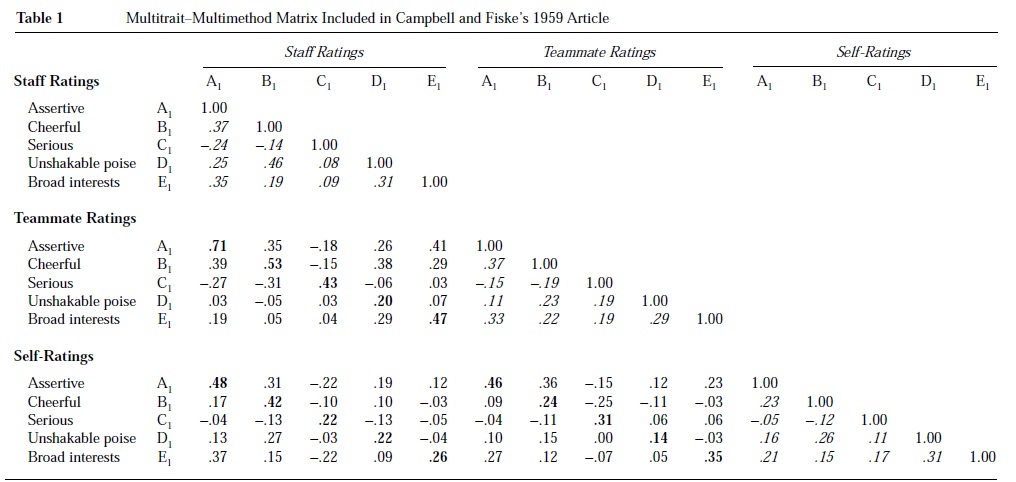
Campbell and Fiske stated that convergent and discriminant validity could be evaluated using four criteria. The first criterion, intended to evaluate convergent validity, is that measures of the same traits by different methods should correlate reasonably highly. These correlations are shown in Table 1 (in the “validity diagonals”) in bold. The staff-teammate same-trait, different-method correlations average .47, which seems reasonable. Convergence between self-ratings and the two other methods is lower; the mean correlations are .32 for staff-self and .30 for teammate-self. Convergent validity is therefore fairly good, at least for staff and teammate ratings.
The other three criteria are aimed at evaluating discriminant validity. The second criterion is that the same-trait, different-method correlations should be higher than the different-trait, different-method correlations that surround them (shown in Table 1 in regular font). This criterion is generally met in Table 1; same-trait, different-method correlations are almost always higher than the different-trait correlations in the same columns and rows (even for self-ratings). Third, the same-trait, different-method correlations (on the validity diagonals) should be higher than correlations for different traits measured by the same method. The different-trait, same-method correlations are shown in italics. Again, the MTMM matrix in Table 1 generally meets this criterion.
Fourth, the various sets of different-trait correlations should all show the same pattern of correlations. These sets include, for example, different-trait correlations for staff (near the top of the MTMM matrix), correlations between staff and teammates (below the staff correlations), and correlations between staff and self-ratings (below staff-teammate ratings). For example, in Table 1, all correlations between assertive and cheerful are positive, indicating that assertive people tend to be cheerful, whereas all correlations between cheerful and serious are negative, indicating a slight tendency for serious people to be less cheerful. Evaluation of this criterion is more subjective and involves comparing many correlations. Finally, the matrix in Table 1 was chosen by Campbell and Fiske because it demonstrates good convergent and discriminant validity. Many matrixes studied by industrial and organizational psychologists (and by researchers in other fields) have shown poorer results.
Recently, flaws in Campbell and Fiske’s analysis procedures have been identified. For example, researchers have had to subjectively evaluate how well the criteria are met because there are no procedures for quantifying the criteria; the correlations in the matrix are influenced by how reliably the variables are measured; and there is no procedure for separating method effects from random errors of measurement. Since the publication of the original article in 1959, a variety of statistical methods have been suggested to overcome these problems. Currently, there is no consensus that there is any single best way to analyze MTMM matrixes, but one approach that has gained popularity is confirmatory factor analysis.
Confirmatory factor analysis provides quantitative methods for evaluating Campbell and Fiske’s criteria, takes into account the reliability of the measures, and separates method effects from random errors. It deals with variation in each measure (e.g., ratings of extroversion), which simply means that some people are rated as more extroverted and others as less extroverted. This variation is conceived as a combination of three factors: (a) variation resulting from the trait (i.e., real differences in extroversion); (b) variation resulting from method effects (i.e., systematic factors unrelated to real differences—for example, a self-rater’s desire to be extroverted rather than his or her actual extroversion); and (c) variation resulting from random factors (e.g., the rater’s mood at the particular moment of rating).
The analysis estimates how much of the total variation results from each of the three factors. This is done separately for each measure by calculating the loadings of each measure on (a) its trait factor (e.g., a loading of an extroversion self-rating on the extroversion factor; extroversion ratings from other sources would also have loadings on this factor); (b) its method factor (all self-ratings, including the self-rating of extroversion, would load on the self method factor); and (c) a random factor (each measure has its own random factor).
The confirmatory factor analysis results provide information similar to that provided by Campbell and Fiske’s criteria—for example, the higher the same-trait, different-method correlations, the higher the trait factor loadings will be, indicating convergent validity. The confirmatory approach removes subjectivity by using statistical significance testing to determine whether there is significant convergent validity (trait variance) and significant method variance. It also quantifies how large the trait versus method effects are. This information can be useful for determining how “good” a measure is and which measures need to be improved (generally speaking, it is desirable to have high trait effects and small method and random error effects).
The confirmatory factor analysis approach does have its shortcomings. The sources listed in the References: section may be consulted for more information on this topic, as well as for other analysis methods.
References:
- Campbell, D. T. (1992). Citations do not solve problems. Psychological Bulletin, 112, 393-395.
- Campbell, D. T., & Fiske, D. W. (1959). Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin, 56, 81-105.
- Kenny, D. A. (1995). The multitrait-multimethod matrix: Design, analysis, and conceptual issues. In P. E. Shrout and S. T. Fiske (Eds.), Personality, research, methods, and theory: A festschrift honoring Donald W. Fiske (pp. 111-124). Hillsdale, NJ: Lawrence Erlbaum.
- Lance, C. E., Noble, C. L., & Scullen, S. E. (2002). A critique of the correlated trait-correlated method and correlated uniqueness models for multitrait-multimethod data. Psychological Methods, 7, 228-244.
- Marsh, H. W. (1989). Confirmatory factor analyses of multitrait-multimethod data: Many problems and a few solutions. Applied Psychological Measurement, 13, 335-361.
- Schmitt, N., & Stults, D. M. (1986). Methodology review: Analysis of multitrait-multimethod matrices. Applied Psychological Measurement, 10, 1-22.