Meta-analysis uses statistical techniques to summarize results from different empirical studies on a given topic to learn more about that topic. In other words, meta-analyses bring together the results of many different studies, although the number of studies may be as small as two in some specialized contexts. Because these quantitative reviews are analyses of analyses, they are literally meta-analyses. The practice is also known as research synthesis, a term that more completely encompasses the steps involved in conducting such a review. Meta-analysis might be thought of as an empirical history of research on a particular topic, in that it tracks effects that have accumulated across time and attempts to show how different methods that researchers use may make their effects change in size or in direction.
Meta-Analysis Rationale and Procedures
As in any scientific field, social psychology makes progress by judging the evidence that has accumulated. Consequently, literature reviews of studies can be extremely influential, particularly when meta-analysis is used to review them. In the past three decades, the scholarly community has embraced the position that reviewing is itself a scientific method with identifiable steps that should be followed to be most accurate and valid.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
At the outset, an analyst carefully defines the variables at the center of the phenomenon and considers the history of the research problem and of typical studies in the literature. Usually, the research problem will be defined as a relation between two variables, such as the influence of an independent variable on a dependent variable. For example, a review might consider the extent to which women use a more relationship-oriented leadership style compared with men. Typically, the analyst will also consider what circumstances may change the relation in question. For example, an analyst might predict that women will lead in a style that is more relationship-oriented than men and that this tendency will be especially present when studies examine leadership roles that are communal in nature (e.g., nurse supervisor, elementary principal).
Analysts must next take great care to decide which studies belong in the meta-analysis, the next step in the process, because any conclusions the meta-analysis might reach are limited by the methods of the studies in the sample. As a rule, meta-analyses profit by focusing on the studies that use stronger methods, although which particular methods are “stronger” might vary from area to area. Whereas laboratory-based research (e.g., social perception, persuasion) tends to value internal validity more than external validity, field-based research (e.g., leadership style, political attitudes) tends to reverse these values.
Ideally, a meta-analysis will locate every study ever conducted on a subject. Yet, for some topics, the task can be quite daunting because of sheer numbers of studies available. As merely one example, in their 1978 meta-analysis, Robert Rosenthal and Donald B. Rubin reported on 345 studies of the experimenter expectancy effect. It is important to locate as many studies as possible that might be suitable for inclusion using as many techniques as possible (e.g., computer and Internet searches, e-mails to active researchers, consulting reference lists, manual searching of related journals). If there are too many studies to include all, the analyst might randomly sample from the studies or, more commonly, narrow the focus to a meaningful subliterature.
Once the sample of studies is in hand, each study is coded for relevant dimensions that might have affected the study outcomes. To permit reliability statistics, two or more coders must do this coding. In some cases, an analyst might ask experts to judge methods used in the studies on particular dimensions (e.g., the extent to which a measure of leadership style is relationship-oriented). In other cases, an analyst might ask people with no training for their views about aspects of the reviewed studies (e.g., the extent to which leadership roles were communal).
To be included in a meta-analysis, a study must offer some minimal quantitative information that addresses the relation between the variables (e.g., means and standard deviations for the compared groups, F-tests, t-tests). Standing alone, these statistical tests would reveal little about the phenomenon.
When the tests appear in a single standardized metric, the effect size, the situation typically clarifies dramatically. The most common effect sizes are d (the standardized mean difference between two groups) and r (the correlation coefficient gauging the association between two variables). Each effect size receives a positive or negative sign to indicate the direction of the effect. As an example, a 1990 meta-analysis that Blair T. Johnson and Alice H. Eagly conducted to examine gender differences in leadership style defined effect sizes in such a way that positive signs were stereotypic (e.g., women more relationship-oriented) and negative signs were counterstereotypic (e.g., men more relationship-oriented). Typically, d is used for comparisons of two groups or groupings (e.g., gender differences in leadership style) and r for continuous variables (e.g., self-esteem and attractiveness).
Then, the reviewer analyzes the effect sizes, first examining the mean effect size to evaluate its magnitude, direction, and significance. More advanced analyses examine whether differing study methods change, or moderate, the magnitude of the effect sizes. In all of these analyses, sophisticated statistics help show whether the studies’ effect sizes consistently agree with the general tendencies. Still other techniques help reveal which particular studies’ findings differed most widely from the others, or examine the plausibility of a publication bias in the literature. Inspection for publication bias can be especially important when skepticism exists about whether the phenomenon under investigation is genuine. In such cases, published studies might be more likely to find a pattern than would unpublished studies. For example, many doubt the existence of so-called Phi effects, which refers to “mind reading.” Any review of studies testing for the existence of Phi would have to be sensitive to the possibility that journals may tend to accept confirmations of the phenomenon more than disconfirmations of it.
Various strategies are available to detect the presence of publication bias. As an example, Rosenthal and Rubin’s fail-safe N provides a method to estimate the number of studies averaging nonsignificant that would change a mean effect size to being nonsignificant. If the number is large, then it is intuitively implausible that publication bias is an issue. Other, more sophisticated techniques permit reviewers to infer what effect size values non-included studies might take and how the inclusion of such values might affect the mean effect size. The detection of publication bias is especially important when the goal of the meta-analytic review is to examine the statistical significance or the simple magnitude of a phenomenon. Publication bias is a far less pressing concern when the goal of the review is instead to examine how study dimensions explain when the studies’ effect sizes are larger or smaller or when they reverse in their signs. Indeed, the mere presence of wide variation in the magnitude of effect sizes often suggests a lack of publication bias.
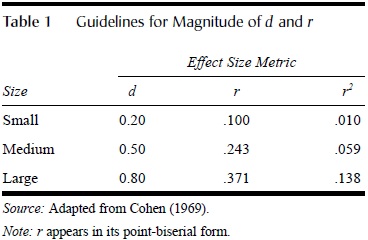
Interpretation and presentation of the meta-analytic findings is the final step of the process. One consideration is the magnitude the mean effect sizes in the review. In 1969, Jacob Cohen informally analyzed the magnitude of effects commonly yielded by psychological research and offered guidelines for judging effect size magnitude. Table 1 shows these standards for d, r, and r2; the latter statistic indicates the extent to which one variable explains variation in the other. To illustrate, a small effect size (d = 0.20) is the difference in height between 15- and 16-year-old girls, a medium effect (d = 0.50) is difference in intelligence scores between clerical and semiskilled workers, and a large effect (d = 0.80) is the difference in intelligence scores between college professors and college freshmen. It is important to recognize that quantitative magnitude is only one way to interpret effect size.
Even very small mean effect sizes can be of great import for practical or applied contexts. In a close race for political office, for example, even a mass media campaign with a small effect size could reverse the outcome.
Ideally, meta-analyses advance knowledge about a phenomenon not only by showing the size of the typical effect but also by showing when the studies get larger or smaller effects, or by showing when effects reverse in direction. At their best, meta-analyses test theories about the phenomenon. For example, Johnson and Eagly’s meta-analysis of gender differences in leadership style showed, consistent with their social-role theory hypothesis, that women had more relationship-oriented styles than men did, especially when the leadership role was communal in nature.
Meta-analyses provide an empirical history of past research and suggest promising directions for future research. As a consequence of a carefully conducted meta-analysis, primary-level studies can be designed with the complete literature in mind and therefore have a better chance of contributing new knowledge. In this way, science can advance the most efficiently to produce new knowledge.
References:
- Cohen, J. (1969). Statistical power analysis for the behavioral sciences. New York: Academic Press.
- Cooper, H. M., & Hedges, L. V. (Eds.). (1994). The handbook of research synthesis. New York: Russell Sage.
- Johnson, B. T., & Eagly, A. H. (2000). Quantitative synthesis of social psychological research. In H. T. Reis & C. M. Judd (Eds.), Handbook of research methods in social and personality psychology (pp. 496-528). London: Cambridge University Press.
- Lipsey, M. W., & Wilson, D. B. (2001). Practical meta-analysis. Thousand Oaks, CA: Sage.
Read More: