Path Analysis Definition
 Path analysis is a statistical technique that is used to examine and test purported causal relationships among a set of variables. A causal relationship is directional in character, and occurs when one variable (e.g., amount of exercise) causes changes in another variable (e.g., physical fitness). The researcher specifies these relationships according to a theoretical model that is of interest to the researcher. The resulting path model and the results of the path analysis are usually then presented together in the form of a path diagram.
Path analysis is a statistical technique that is used to examine and test purported causal relationships among a set of variables. A causal relationship is directional in character, and occurs when one variable (e.g., amount of exercise) causes changes in another variable (e.g., physical fitness). The researcher specifies these relationships according to a theoretical model that is of interest to the researcher. The resulting path model and the results of the path analysis are usually then presented together in the form of a path diagram.
Although a path analysis makes causal inferences about how variables are related, correlational data are actually used to conduct the path analysis. In many instances, the results of the analysis provide information about the plausibility of the researcher’s hypothesized model. But even if this information is not available, the path analysis provides estimates of the relative strengths of the causal effects and other associations among the variables in the model. These estimates are more useful to the extent that the researcher’s specified model actually represents how the variables are truly related in the population of interest.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
Variables in Path Analysis
Path analysis is a member of a more general type of statistical analysis known as structural equation modeling. The feature of path analysis that separates it from general structural equation modeling is that path analysis is limited to variables that are measured or observed, rather than latent. This means that each variable in a path analysis consists of a single set of numbers in a straightforward way. For example, extra-version would be considered a measured or observed variable if each person’s level of extraversion was represented by a single number for that person, perhaps that person’s score on an extraversion questionnaire. So the variable of extraversion as a whole would consist of one number for each person in the sample. Through certain statistical techniques, extraversion could be treated as a latent variable in a structural equation model by using several different measures simultaneously to represent each person’s level of extraversion. But by definition, path analysis does not use latent variables.
Model Specification
The researcher must begin a path analysis by specifying the ways in which the variables of interest are thought to relate to one another. This is done based on theory and reasoning, and it is critical that the researcher specify the model thoughtfully. A key aspect of this process is deciding which particular variables causally affect other particular variables. A model in which exercise causes good health has a very different meaning than a model in which good health causes exercise. But in many instances, the numeric results of such alternative path analyses will reveal little or nothing about which model is closer to the truth. Because of this, there is no substitute for the researcher having a sound rationale for the form of the path model.
Path Diagrams
The path diagram is a visual display of the path model and the results of the path analysis. In path diagrams, measured variables are usually represented as squares or rectangles. A single-headed arrow (also known as a path or direct effect) drawn from one variable to another (say, from anxiety to attention seeking; see the standardized path diagram shown in Figure 1) means that a change in the value of anxiety is thought to tend to cause a change in the value of attention seeking (rather than vice versa). It is not necessary for the researcher to specify in advance whether increases in the first variable are thought to cause increases or decreases in the second variable. Mathematical algorithms will estimate both the magnitude of the effect and its positivity or negativity.
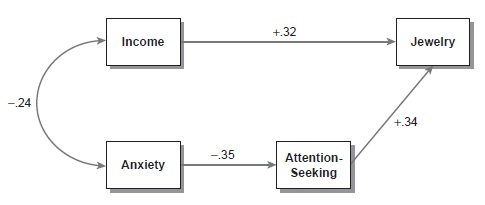
Figure 1 Example Path Analysis Based on Entirely Fictional Data
A double-headed arrow (sometimes known as a correlation in standardized path diagrams, or a covariance in unstandardized diagrams) means that the two connected variables are assumed to be associated with one another (again, either positively or negatively), but with no particular cause assumed (as with income and anxiety). This type of relationship is sometimes referred to as an unanalyzed association because the path model does not address why these two variables are associated. They are simply allowed to associate freely.
Data
Once the researcher has specified the path model, it is necessary to have data available to perform the analysis. The variables in the entirely fictional example of Figure 1 are income (annual income in dollars), anxiety (a score from a psychometric anxiety questionnaire), attention seeking (also a questionnaire score), and impressiveness of jewelry (say, a rating of each person’s jewelry done by a trained coder). What is required is a sample of data in which each of these variables has been measured for each case in the sample. So the researcher would need a sufficiently large group of people for whom values of each of these four variables are available.
The primary inputs to path analysis software are numbers that indicate the strength and the sign (either positive or negative) of the association between each pair of variables. There is one such number for every unique pair of variables. Depending on the form of the analysis, these associations may be referred to as either correlations or covariances. Regardless, a defining feature of this input information is that no causality among the variables is actually implied in these data themselves. They simply index the strength of the association for each pair of variables in the model, and whether it is positive or negative.
Model Fit
The number of variables used in the path analysis imposes a limit on the complexity of the path model. In most instances, a model is as complex as possible if it has as many paths and correlations as there are unique pairs of variables. Models such as these are known as just-identified models. This is not, however, to imply that more complex models are necessarily more desirable; more complex models are less parsimonious.
In Figure 1, there are four variables and thus 4(4–1)/2 = 6 unique pairs of variables. Because there are fewer paths and correlations in Figure 1 than unique pairs of variables, this model is not just-identified. Models such as this are known as overidentified models. A desirable property of overidentified models is that the path analysis can typically provide information about model fit. The most basic piece of this information is known as the chi-square statistic. To the extent that the probability value associated with this statistic is relatively low, it is improbable that the researcher has specified a path model that is correct in the population from which the sample data came. In other words, the researcher is confronted with evidence that the specified model is untenable as a representation of what is really happening in the population.
Indices of model appropriateness besides the chi-square statistic are available and are commonly used. This is partly because many researchers regard the chi-square statistic as too stringent a test for structural equation models in general. Use of these alternative fit indices is associated with a lower likelihood of rejecting a researcher-specified model. The extent to which fit information from the chi-square statistic should counterbalance the generally more lenient criteria of other indices is a controversial issue. Regardless of how a researcher chooses to emphasize each type of fit information, it is important to know that they are only available for overidentified models. Furthermore, it is important to understand that even though poor model fit means that the model specified by the researcher is likely inaccurate, good fit in no way guarantees the correctness of the model. For example, the researcher could have omitted important variables or misspecified the direction of one or more causal arrows, yet still possibly have good fit.
Path Coefficients
All path analyses provide estimates of the values of the paths and correlations that connect the observed variables. Though the researcher specifies the presence or absence of particular paths and correlations, the specific values of these coefficients are entirely calculated by the mathematical algorithms of path analysis acting on the sample data. They are mathematical best available estimates of what the coefficients would be if the entire population were available for analysis. These values are typically displayed in the diagram next to the appropriate path (see Figure 1).
Standardized (as opposed to unstandardized) coefficients are typically presented in path diagrams. The use of standardized coefficients attempts to allow comparisons of the relative strengths of the paths and correlations even though the variables involved may have very different scales of measurement. These standardized coefficients can range in value from -1.00 to +1.00. Greater absolute values indicate stronger relationships, and the sign (+ or -) indicates whether an increase in a causal variable results in a predicted increase (+) or decrease (-) in a caused variable or whether a correlation is positive or negative.
Changing the direction of an arrow, eliminating it, replacing it with a correlation, or changing the variables included in the model can result in different values for the strength of that path and can affect other paths in the model in unpredictable ways. Relatedly, in a path analysis with three or more variables, a path from variable X to variable Y might have a very different strength or even a different sign (+ versus -) than what might be expected from looking at the simple association between X and Y alone. For these reasons, path analysis can be a very informative technique. But whether it is informative or misleading depends on the soundness of the researcher’s model and the representativeness of the sample data.
In Figure 1, the correlation of income and anxiety is -.24, meaning that higher incomes are associated with lower levels of anxiety in these sample data. The value of +.32 for the path from income to jewelry means that increasing income is predicted to directly cause increases in the impressiveness of people’s jewelry. Importantly, this model asserts that income can be thought to relate to the impressiveness of people’s jewelry in two separate ways. Although income exerts a direct effect (+.32) on jewelry, it is also spuriously associated with jewelry via its correlation with anxiety because anxiety causes changes in attention seeking, which in turn causes changes in jewelry. The path analysis has decomposed the original, singular sample association between income and jewelry into these two conceptually distinct parts based on the researcher’s theoretical model and the sample data. Theory-based decompositional inferences such as this are the essence of path analysis.
Note also that anxiety is not directly linked to jewelry in this model. Thus, this model asserts that the association between these variables in the population can be entirely accounted for via income and attention seeking. To the extent that this theoretical assertion had been wrong, indices of model fit would tend to be worse.
References:
- Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. Mahwah, NJ: Erlbaum.
- Keith, T. Z. (2006). Multiple regression and beyond: A conceptual introduction to multiple regression, confirmatory factor analysis, and structural equation modeling. Boston: Allyn & Bacon.
- Kline, R. B. (1998). Principles and practice of structural equation modeling. New York: Guilford Press.
- Wonnacott, T. H., & Wonnacott, R. J (1981). Regression: A second course in statistics. New York: Wiley.
Read More: