Along with the operationally defined concepts of dynamical systems theory comes a rich arsenal of mathematical methods and modeling tools that may be usefully employed in the study of complex sports behaviors. This entry highlights just a handful of those, which are all centered on the “problem” of dimensionality reduction. Before going into modeling, the entry first outlines some useful approaches to data analysis aimed at system identification, starting with more heuristic approaches that capitalize on an educated guess about which state variable is (most) relevant, followed by more unbiased, statistical approaches.
System Identification
Parameter Extraction: Stability and Regularity
When seeking to identify the main characteristics of a system’s dynamics, one typically applies conventional statistics in combination with stability-related measures like Lyapunov or Floquet exponents. Lyapunov exponents are the method of choice in estimating the stability properties of a dynamical system involving the emergence and disappearance of macroscopic patterns, such as the transitions from walking to running, and from ankle to hip strategy in upright posture.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
The Lyapunov exponent measures the exponential divergence of nearby trajectories and thus the robustness of a (movement) pattern against (small) perturbations. Only if the exponential divergence is negative, a perturbation will be compensated and the pattern is (locally) stable; otherwise, a transition is likely to occur or is permanently present (as in chaotic systems or self-organized criticality). In the study of movement coordination, Lyapunov exponents and other stability-related measures have proved rather useful in addressing movement flexibility, stability, and adaptability.
Of similar importance for the identification of dynamics are entropic measures. In physics, entropy is used to quantify the degree of disorder in a statistical ensemble such as a gas. When looking at movement trajectories, in contrast, entropy may serve to quantify the degree of regularity. A frequently used measure in the analysis of noisy time series, such as movement data, is sample entropy. Entropic measures have been used, among others, to assess balance in gymnastics and dance, and the effects of sports-related anxiety and brain injury on postural control. Entropy can be readily estimated, irrespective of the type and dimensionality of the data in question. For instance, predictability of competitive balance in sporting contests has been assessed through entropy using the example of the 2006–2007 English Premier League results.
Dimensionality Reduction: Principal Component Analysis and More
Advances in data acquisition have allowed for simultaneous recordings of multiple signals for considerable time spans, resulting in huge data sets. This development has increased the need of a priori data reduction. Principal component analysis (PCA) suits this purpose.
When analyzing movement, an estimate of the covariance matrix between trajectories (or time series) is central to PCA. Eigenvalues of this covariance matrix rank the degree to which a so-called principal component contributes to the entire data variance (which provides an index of its strength). The corresponding eigenvectors are the principal components, also referred to as factor loadings. When projected onto these components, the movement trajectories yield factor scores (here the time series of the components). PCA has found wide application in sports, and many examples may be found in the literature.
Alternative but related approaches include, for example, clustering techniques and artificial neural networks, which all pursue the same goal: reducing dimensionality. However, an even more principled and rigorous approach to pursue that goal is to focus on phase transitions because theory dictates that in the immediate vicinity of the critical point the dynamics of the complex system under study is reduced to a (small) set of order parameters. Whenever that scenario occurs, mathematical modeling in terms of dynamical systems becomes feasible.
Identifying Dynamics: Capitalizing on Noise
This section highlights a recently established method for identifying stochastic dynamics. Originally, this analysis had been developed to study stochastic processes in the context of turbulent flows, but of late, it has also been applied successfully in the analysis of a broad variety of experimental data including human movement. The method produces numerical values of dynamical equations as a function of phase space coordinates. From these numerical values, specific model terms can be estimated, but they can also be analyzed directly by reconstructing vector fields and comparing those across experimental conditions; see Figure 1.
Modeling
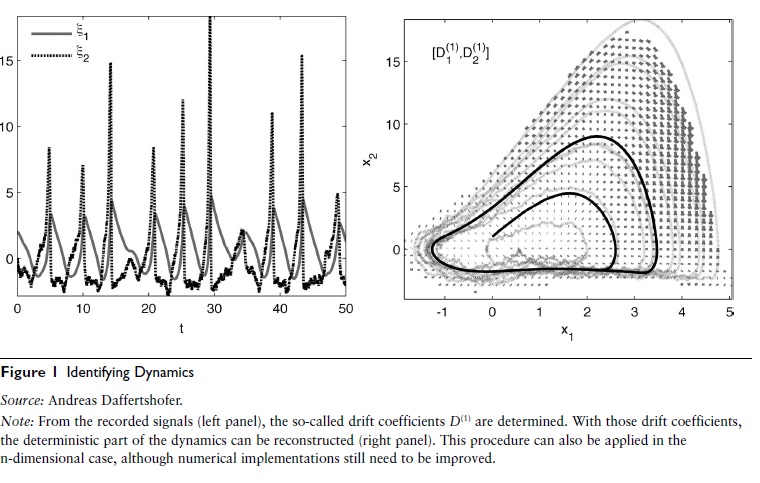 Figure 1 Identifying Dynamics
Figure 1 Identifying Dynamics
To model a complex dynamical system, consider xkas state variable dependent on time t. Further, let the system be high-dimensional (e.g., of dimension n) such that the entire system can be cast inthe vector-form X = (x1, x2, . . . , xn). Its stochastic dynamics may then read
= F(X, t) + noise, (1)
where the dot-notation refers to the derivative with respect to time. In the presence of phase transitions one can split the state variables into those that become unstable (u, representing the switch in macroscopic patterns) and those that stay stable (s). One may formally write X = (u, s). The previously explained separation of time scales in the vicinity of the phase transition implies that the stable parts can be eliminated adiabatically,1which somewhat counterintuitively has the mathematical form = 0. This adiabatic elimination allows for expressing the stable components as mere functions of the unstable ones, i.e., s = M(u), which known as the center manifold theorem according to which the stable components are “enslaved” by the unstable ones. The latter are hence the so-called order parameters whose dynamics read
= N(u, t) + noise. (2)
Importantly, the dimension of u is always much smaller than that of X by which one can the rigorously analyze the system X through well-established mathematical techniques.
As an example, consider the case in which the order parameter dynamics can be written using the gradient of a potential V—that is, = –V’(u). If V is depicted as a landscape, then the systems stability can be readily determined by means of the hills and valleys of the landscape: the former represent the unstable states and the latter the stable states of the dynamics.
Movement Coordination: Low-Dimensional Dynamics
The previously given approach had a major impact on the study of the coordination of rhythmic movement through the seminal work of J. A. Scott Kelso and colleagues on frequency-induced phase transitions in rhythmic finger movements. This transition was modeled by means of potential for the relative phase between the finger movements, which changed shape as a function of movement frequency, as shown in Figure 2, and an underlying system of two nonlinearly coupled nonlinear oscillators. The model motivated a flurry of research on rhythmic bimanual coordination, with ramifications to learning and development, the accompanying brain activity, and to interpersonal coordination in dyads and teams. Through the intimate connection between the study of motor systems has found many applications in recent years. Complex networks link to dynamical systems by virtue of the phase transitions that occurwhen a network grows and connections areformed; in random networks, transitions occur control and learning and sports behavior, it also penetrated the domain of sport science.
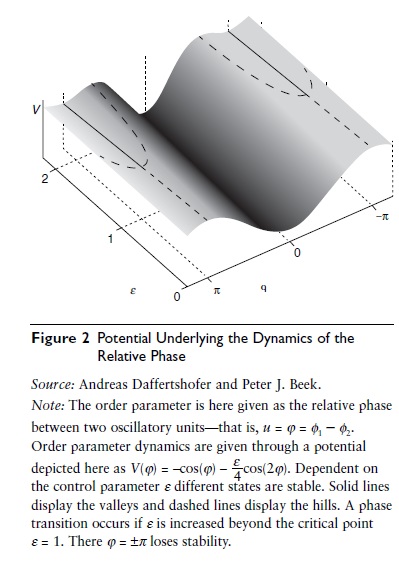
Figure 2 Potential Underlying the Dynamics of the Relative Phase
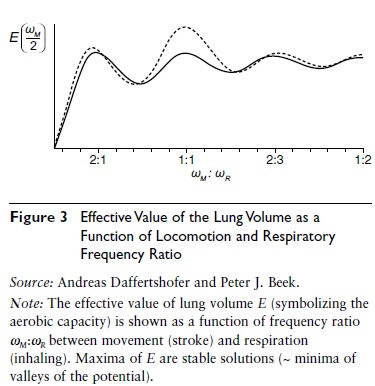 Figure 3 Effective Value of the Lung Volume as a Function of Locomotion and Respiratory Frequency Ratio
Figure 3 Effective Value of the Lung Volume as a Function of Locomotion and Respiratory Frequency Ratio
Entrainment of Locomotion and Respiration— Also Low-Dimensional
A closely related approach revealed how the optimization of oxygen extraction in animal respiration can explain the multi-frequency synchronization of breathing and locomotion observed in competitive rowing. In this case, the to-be-analyzed potential is formed by the negative effective value of lung volume (modulated by the cyclic muscle contraction due to locomotion). The corresponding variational principles (searches for hills and valleys) do not only predict steady—that is, optimal— states but also (points of) transitions between those states whenever control parameters— again, movement speed but also fatigue—are being altered; see Figure 3.
Graph Theory
The analysis of complex networks as a discretized and distributed version of complex toward (almost) fully connected networks dependent on growth rate and the probability to connect. It is duly recognized in the literature that match play in (ball) sports are amenable in terms of an analysis in terms of network theory. And indeed all ingredients for this are available: The players represent the nodes, and they are connected to each other via ball passes and via perception-based collective motion. These connections represent the edges. The number of passes between players provides a strength of their connection and so does—although more difficult to quantify— coherent motion. An analysis of a sports match in those terms is already arguably more revealing than an analysis in more conventional terms like average speed, distance covered, or areas visited. Using a variety of so-called centrality measures, it may provide information about the importance of nodes (hubs) and edges in the network and thus reveal strategic behaviors. Various attempts have been made in this regard, but a crucial element has so far been missing—namely the fact that the connections between players serve the purpose of making and preventing goals, implying that goal effectiveness and directionality should be incorporated into the analysis. In other words, network theory needs to be appropriated to match analysis in order to make it transcend the current divide between match play analyses based on temporal correlations (e.g., relative phase) and spatial correlations (e.g., Voronoi diagrams).
Conclusion
Concepts of dynamical systems build on a potent arsenal of mathematical tools. Exploiting this arsenal yields a highly sophisticated assessment of complex sports performance. Models in motor control are seminal for the predictive capacity of this approach. In particular, the macroscopic switches in behavior can be analyzed with great precision. Like the general focus on dynamical systems in sports science, also modeling efforts are still in their infancies. The rigor of the employed mathematical tools, however, renders the approach comprehensive and appealing.
References:
- Davids, K., Button, C., & Bennett, S. (2008). Dynamics of skill acquisition: A constraints-led approach. Champaign, IL: Human Kinetics.
- Friedrich, R., & Peinke, J. (1997). Description of a turbulent cascade by a Fokker-Planck equation. Physical Review Letters, 78(5), 863–866. doi:10.1103/Physrevlett.78.863
- Haken, H. (1977). Synergetics—An introduction. Berlin: Springer-Verlag.
- Huys, R., & Jirsa, V. K. (2010). Nonlinear dynamics in human behavior. Berlin: Springer.
- Kelso, J. A. S. (1995). Dynamic patterns: The selforganization of brain and behavior. Cambridge: MIT Press.
- van Mourik, A. M., Daffertshofer, A., & Beek, P. J. (2008). Extracting global and local dynamics from the stochastics of rhythmic forearm movements. Journal of Motor Behavior, 40(3), 214–231. doi: 10.3200/ JMBR.40.3.214-231
- Witte, K., Ganter, N., Baumgart, C., & Peham, C. (2010). Applying a principal component analysis to movement coordination in sport. Mathematical and Computer Modelling of Dynamical Systems, 16(5),477–488. doi: 10.1080/13873954.2010.507079
- Yue, Z. Y., Broich, H., Seifriz, F., & Mester, J. (2008).Mathematical analysis of a soccer game. Parts I & II.Studies in Applied Mathematics, 121(3), 223–243,245–261
See also: