For describing or testing hypotheses about a population, sampling a small portion of the population is often preferable to taking a census of the entire population. Taking a sample is usually less expensive and less time-consuming than taking a census and more accurate because more effort and care can be spent ensuring that the right data are gathered in the right way. Data collected appropriately can be used to make inferences about the entire population.
Sampling techniques can be categorized into non-probability samples and probability samples. A probability sample is selected in a way such that virtually all members of a population have a nonzero probability of being included, and that probability is known or calculable. A nonprobability sample is gathered in a way that does not depend on chance. This means that it is difficult or impossible to estimate the probability that a particular unit of the population will be included. Moreover, a substantial proportion of the population is typically excluded. The quality of the sample, therefore, depends on the knowledge and skill of the researcher.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
In general, probability samples are preferable to nonprobability samples because results can be generalized to the entire population using statistical techniques. Such generalization is typically invalid with nonprobability samples because the exclusion of portions of the population from sampling means the results are likely to be biased. People who volunteer to participate in a study, for example, may be different from those who do not; they may differ in age, gender, occupation, motivation, or any number of other characteristics that may be related to the study. If the study concerns attitudes or opinions, volunteer participants may have different and often stronger feelings about the issues than nonparticipants.
Nonprobability samples, however, have their advantages and uses. They are relatively easy and inexpensive to assemble. They can be valuable for exploratory research or when the researcher wants to document a range or provide particular examples rather than investigate tendencies or causal processes. Moreover, techniques have recently been developed for obtaining unbiased results from certain kinds of nonprobability samples.
Two concepts are important to sampling in general: the target population and the sampling frame. The target population is the population to which the researcher wants to generalize the findings. One important characteristic of the population is the kind of entities its members are, known as the unit of analysis. The cases in the sample correspond to this unit of analysis. Examples of a unit of analysis are the individual, the organizational department, the organization, or some geographical unit, such as the state. The unit of analysis is characterized by a set of attributes on which the researcher gathers data. These are the variables the researcher scores for each case in the sample. For example, a researcher might explore individual characteristics such as age or years of education. Usually, the target population is circumscribed by some characteristic or combination of characteristics. It may be employees of a particular firm, or there may be a geographical limitation, such as residents of a particular city. Constraints on gender, ethnicity, age-group, work status, or other characteristics may be specified as well. A target population, for example, might be permanent, full-time female employees of a particular company.
The sampling frame is the complete list of all units from which the sample is taken. For the target population of permanent, full-time female employees, for example, the sampling frame might be a list of permanent, full-time female employees from all of the company’s locations. For telephone surveys, a list of phone numbers is a typical sampling frame, perhaps for particular area codes or in conjunction with block maps.
Probability Samples
Sample Designs
For probability samples, there are four common designs: the simple random sample, the systematic sample, the stratified sample, and the cluster sample. A simple random sample is drawn in such a way that every combination of units of a given size has an equal probability of being drawn. If there are n individuals in the sample and N in the population, for example, each individual’s probability of being included is n/N. The simple random sample is optimal for estimating unbiased population characteristics as precisely as possible. The most commonly used statistical techniques assume and work best with simple random samples. A simple random sample can be drawn by applying a table of random numbers or pseudorandom numbers generated by a computer to the sampling frame. Unfortunately, for many target populations, it is difficult and costly to draw a simple random sample. Hence, researchers use sample designs that approximate simple random samples.
One such design is a systematic sample, which is drawn in such a way that every unit in the target population has the same probability of being selected, but the same is not true for every combination of units of a given size. A systematic sample might be used when the sample frame is a long, noncomputerized list. To carry it out, determine a sampling interval (I) based on the desired sample size (n): I = N/n. Choose at random a starting case, from the first through the Ith units in the list. Then from that starting case, select every Ith unit. A systematic sample will approximate a simple random sample unless there is some sort of periodicity in the sampling frame, which then will lead to bias in the results.
A more controlled sampling design is the stratified sample, which is undertaken to ensure a specified proportional representation of different population groups in the sample. If the target population is 10% Hispanic, for example, a simple random sample drawn from the population may be more or less than 10% Hispanic. A stratified sample ensures that 10% of the sample—or some other desired proportion, say 20%—will be Hispanic. Stratified samples may be classified into proportionate and disproportionate samples. A proportionate stratified sample ensures that the composition of the sample mirrors the composition of the population along some variable or combination of variables. To carry it out, divide the target population into subgroups according to the desired aspect—Hispanic and non-Hispanic, for example. Then take a simple random sample from each subgroup, with the same probability of selection for each subgroup.
In a disproportionate stratified sample, the proportion of different subgroups in the sample is set to differ from that in the target population. Typically, the composition of the sample over represents subgroups that form only a small proportion of the population. The purpose is to improve estimates for that subgroup and improve comparison between subgroups. For example, suppose the sample size is to be 500 and the target population is 5% Hispanic. A simple random sample would include about 25 Hispanic individuals, which is too small to obtain precise estimates for that subgroup. If better estimates are desired, the proportion of Hispanics in the sample can be raised, say to 20%, which will ensure that 100 Hispanic individuals are selected, thus producing more precise estimates for the subgroup and allowing Hispanic and non-Hispanic individuals to be compared more accurately. Analysis of the entire sample should be conducted using weights to adjust for the overrepresentation of some subgroups, a simple option in most major statistical packages for computers.
Cluster sampling is a common method for face-to-face data collection such as surveys. The data are gathered from a small number of concentrated, usually spatially concentrated sets of units. A few departments of an organization may be sampled, for example, or a few locations if an organization has multiple locations. Cluster sampling may be chosen to reduce costs or because there is no adequate sampling frame from which a simple random sample or systematic sample could be drawn.
Sample Size
One question that commonly arises in research is how large a sample is necessary. Collecting data is costly, and it may be better to concentrate on gathering higher-quality data from a smaller sample, if possible. Several methods for estimating the necessary sample size exist. One method is simply to use sample sizes that approximate those of other studies of high quality. Some references contain tables that give appropriate sample sizes.
Two formulas may be of assistance. Let p denote the proportion of the population with a key attribute; if the proportion is unknown, p = .5 (which assumes maximum variability) may be used. Let e denote the sampling error or level of precision, expressed as a proportion. Thus, e = .05 means ± 5% precision. Finally, suppose a confidence level of 95% is desired. The sample size, n0, may be estimated by
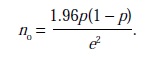
If the key variable takes on more than two values, the best method may be to dichotomize it—that is, transform it into a variable that takes two values—and then estimate p. Otherwise, p =.5 may be used, which gives a conservative estimate of sample size. For smaller populations (in the thousands, for example), wherein population size is denoted by N, the formula
![]()
may be used.
Other considerations may also affect the determination of the necessary sample size. If the researcher wishes to analyze subgroups of the target population separately or compare subgroups, then the sample must be large enough to represent each subgroup adequately. Another concern is nonresponse. Inevitably, not all units in the selected sample will provide usable data, often because they refuse or are unable to participate but also because of respondent error. Here, too, the sample must be large enough to accommodate nonresponses and unusable responses. Finally, money and time costs are a constraint in sampling and should be considered in planning the study so that the sampling can be completed as designed.
Nonprobability Samples
Haphazard, convenience, quota, and purposive samples are the most common kinds of nonprobability samples. Convenience samples comprise units that are self-selected (e.g., volunteers) or easily accessible. Examples of convenience samples are people who volunteer to participate in a study, people at a given location when the population includes more than a single location, and snowball samples. A snowball or respondent-driven sample is one in which the researcher begins with certain respondents, called “seeds,” and then obtains further respondents through previous respondents. A quota sample is one in which a predetermined number of units with certain characteristics are selected. For a purposive sample, units are selected on the basis of characteristics or attributes that are important to the evaluation. Many focus groups are samples of this kind.
Recently, advances have been made in obtaining unbiased results for populations from which probability samples cannot be drawn directly, typically because no adequate sampling frame is available. A hypernetwork method can be applied to a target population of objects or activities that are linked to people—for example, art objects or arts-related activities. A probability sample of the individuals can then be used to obtain a probability sample of organizations providing those objects or activities. Another method again uses the techniques of social network analysis to obtain unbiased estimates from respondent-driven samples. This method is especially helpful in estimating characteristics of hidden populations, such as the homeless or drug users in a particular location.
References:
- Cochran, W. G. (1977). Sampling techniques. New York: Wiley.
- Kish, L. (1965). Survey sampling. New York: Wiley. McPherson, M. (2001). Sampling strategies for the arts: A hypernetwork approach. Poetics, 28, 291-306.
- Miaoulis, G., & Michener, R. D. (1976). An introduction to sampling. Dubuque, IA: Kendall/Hunt.
- Salganik, M. J., & Heckathorn, D. (2004). Sampling and estimation in hidden populations using respondent-driven sampling. Sociological Methodology, 34, 193-240.